Statistical Fraud in The FDA Vaccine Approval Process?
The Pfizer vaccine was approved by the FDA on August 23rd, a very fast track approval process when compared to other vaccines. I suspect the political pressures were enormous. But still, how can approval be possible when the safety record of this vaccine is far worse than any vaccine in the past, including many that were pulled from the market?
Part of the answer is that CDC is not reporting the statistic most relevant to measuring efficacy. That is: Vaccination status of COVID patients. How many of the new infections and new deaths are in vaccinated individuals, and how many in unvaccinated? Of course, this information is known in CDC databases; it is scandalous that the numbers are not being made public. I do not know if they are being provided to FDA. Israel is more honest, and numbers from there are not encouraging.
Likewise, data about transmissibility, comparing vaccinated and unvaccinated populations, are not being reported, and were not part of the clinical trials last fall.
When it comes to safety, there are several systems for reporting vaccine reactions, including deaths, but the only one available to the public is VAERS. It is incomplete, because it relies on voluntary reporting, there is no incentive to report to VAERS, and it is a cumbersome process.
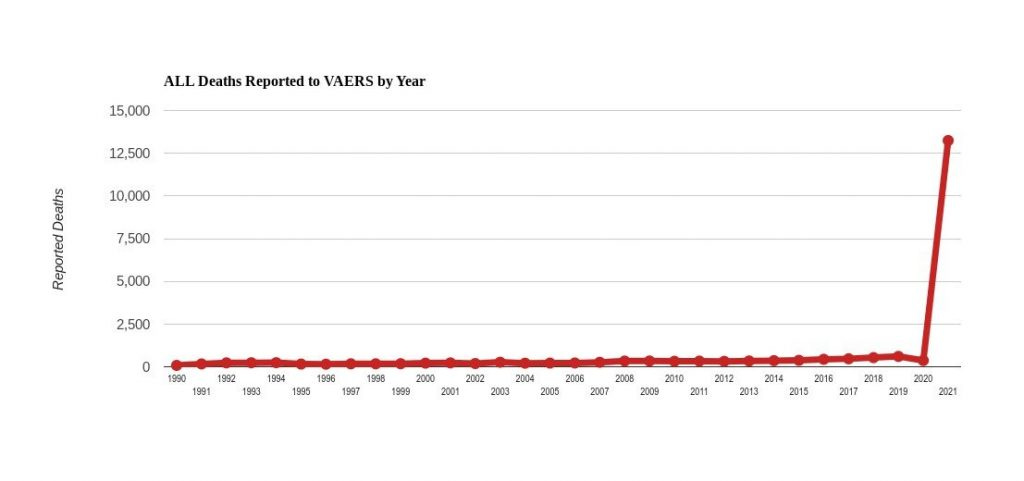
We may compare reports of the COVID vaccines to past years, when there were also hundreds of millions of vaccinations, including annual flu shots and childhood vaccine schedules. The comparison is dramatic.
There were more than twice as many deaths related to the COVID vaccines this year as the sum total of all vaccine deaths in the 30-year history of VAERS.
Given this safety record, how is there any possibility of approval? Here is where the statistical fraud comes in. [I am grateful to have been alerted to this situation by Matthew Crawford]
The safety criterion they have chosen is an obscure computation called PRR for Proportional Reporting Ratio. As the name implies, it is based on RATIOS of different event types and is utterly blind to the ABSOLUTE RATE of such events.
PRR measures the distribution of different kinds of adverse events, e.g. blood clots, heart attacks, and deaths. If those ratios are severely out of line with the great variety of vaccine reactions in the past, PRR would detect that.
For example, if the new vaccines caused an extraordinary risk of myocarditis, but everything else was low, then PRR would flag that. But if myocarditis was just one risk among many that have been reported from past vaccines, then PRR would not pick that up.
The real scandal is that PRR is blind to the absolute risk numbers. PRR is defined in such a way as to look for unusual PATTERNS of adverse events, but it is completely insensitive to unusual RATES of adverse events. Of course, it is the rates and not the patterns that are of primary concern, and the PRR is designed NOT to reflect that.
For example, suppose we have 2 vaccines:
Vaccine A has 1 reported death per million vaccinations, 3 reported heart attacks per million, and 20 reported headaches per million.
Vaccine B has 1 reported death per hundred vaccinations, 3 reported heart attacks per hundred, and 20 reported headaches per hundred.
Vaccine A is quite safe, and vaccine B is extremely dangerous. And yet the formula for PRR will produce the same result for vaccine A and B!
Clearly, PRR is not an appropriate criterion for evaluating safety of any particular vaccine. Someone might assume that PRR was used to cook the books.